Lecture 1: Feature Matching Code
Contents
Lecture 1: Feature Matching Code #
#@title
from ipywidgets import widgets
out1 = widgets.Output()
with out1:
from IPython.display import YouTubeVideo
video = YouTubeVideo(id=f"Bcm264VX6r8", width=854, height=480, fs=1, rel=0)
print("Video available at https://youtube.com/watch?v=" + video.id)
display(video)
display(out1)
#@title
from IPython import display as IPyDisplay
IPyDisplay.HTML(
f"""
<div>
<a href= "https://github.com/DL4CV-NPTEL/Deep-Learning-For-Computer-Vision/blob/main/Slides/Week_3/DL4CV_Week03_Part01.pdf" target="_blank">
<img src="https://github.com/DL4CV-NPTEL/Deep-Learning-For-Computer-Vision/blob/main/Data/Slides_Logo.png?raw=1"
alt="button link to Airtable" style="width:200px"></a>
</div>""" )
Regression with RANSAC for Robust curve fitting#
For a given polynomial, \ $\(y_{i}=\beta_{0}+\beta_{1} x_{i}+\beta_{2} x_{i}^{2}+\cdots+\beta_{m} x_{i}^{m}+\varepsilon_{i}(i=1,2, \ldots, n)\)$
we can express it in a form of matrix \(\mathbf{X}\), a response vector or \(\vec{y}\), a parameter vector \(\vec{\beta}\), and a vector \(\vec{\varepsilon}\) of random errors. The model can be represented as system of linear equations, i.e.
\[\begin{split}\left[\begin{array}{c}y_{1} \\ y_{2} \\ y_{3} \\ \vdots \\ y_{n}\end{array}\right]=\left[\begin{array}{ccccc}1 & x_{1} & x_{1}^{2} & \ldots & x_{1}^{m} \\ 1 & x_{2} & x_{2}^{2} & \ldots & x_{2}^{m} \\ 1 & x_{3} & x_{3}^{2} & \ldots & x_{3}^{m} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & x_{n} & x_{n}^{2} & \ldots & x_{n}^{m}\end{array}\right]\left[\begin{array}{c}\beta_{0} \\ \beta_{1} \\ \beta_{2} \\ \vdots \\ \beta_{m}\end{array}\right]+\left[\begin{array}{c}\varepsilon_{1} \\ \varepsilon_{2} \\ \varepsilon_{3} \\ \vdots \\ \varepsilon_{n}\end{array}\right]\end{split}\]
\[or\]
\[\vec{y}=\mathbf{X} \vec{\beta}+\vec{\varepsilon}\]
For this system, we can calculate \(\vec{\beta}\) by using the following formula, $\( \widehat{\vec{\beta}}=\left(\mathbf{X}^{\top} \mathbf{X}\right)^{-1} \mathbf{X}^{\top} \vec{y} \)$
Using RANSAC, we want to avoid outliers in our curve fitting, and thus we will calculate multiple \(\vec{\beta_i}\)s using a set of datapoints. After calculating several \(\vec{\beta_i}\) we will find the best value of \({\beta}\) using least squares.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import mean_squared_error
from sklearn.utils.random import sample_without_replacement
class Regression:
def __init__(self,order,bias=True):
"""
Initialize regressor
:param order: order of the polynomial
:param bias: boolean, True for our case
"""
# Initializing variables
self.order = order
self.bias = bias
self.beta = np.zeros(order + bias)
self.iterations = 0
self.prob = 0.99
# Predict equation using polyfit
def predict(self, x):
poly_eqn = np.poly1d(self.beta)
y_hat = poly_eqn(x)
return y_hat
def solve(self,x,y,n,iterations=10000):
'''
Function to solve regression using RANSAC
:param x: input
:param y: output
:param n: number of dataset per iteration
:param iterations: number of iterations to find best beta
'''
# Generate random seed
seed = np.random.RandomState(0)
# Initialize variables
close_points = 1
best_err = np.inf
self.best_coord = None
best_fit_x = None
best_fit_y = None
self.max_itr = iterations
self.threshold = np.median(np.abs(y - np.median(y)))
# Initialize coordinate array
x_coord = np.array([i for i in range(len(x))])
# Loop for maximum number of iterations
while self.iterations < self.max_itr:
# Sample random points to be inliers
maybeInliers = sample_without_replacement(len(x), n, random_state=seed)
# Find the coefficients for this model
self.beta = np.polyfit(x, y, self.order)
# Find the equation for model and errors
maybeModel = self.predict(x)
error = np.abs(y - maybeModel)
# Find coordinates of points having error less than threshold
coord = np.zeros(len(error), dtype=bool)
for i in range(0,len(error)):
if (error[i] <= self.threshold):
coord[i] = True
# Find also inlier points
alsoInliers = x_coord[coord]
len_alsoInliers = len(alsoInliers)
# If number of inlier points are greater
if (len_alsoInliers >= close_points):
# Find mean squared error in new and old model
model_err = mean_squared_error(y[alsoInliers], self.predict(x[alsoInliers]))
# If error for current model is less and have more points
if (len_alsoInliers > close_points or model_err < best_err):
# Update model parameters
close_points = len_alsoInliers
best_err = model_err
self.best_coord = coord
best_fit_x = x[alsoInliers]
best_fit_y = y[alsoInliers]
# Update maximum iterations
w = close_points / float(len(x))
if (self.prob != 0 and w != 0):
k = np.log(1 - self.prob) / np.log(1 - w**n)
k = abs(float(np.ceil(k)))
self.max_itr = min(self.max_itr, k)
# Increase iterations
self.iterations += 1
# Find final coefficients
self.beta = np.polyfit(best_fit_x, best_fit_y, self.order)
return self.beta,best_err
def visualize(self, x, y, y_ransac, show=True):
'''
function to visualize datapoints and optimal solution.
'''
# Plot figures
plt.figure(figsize =(12, 8), dpi = 100)
plt.plot(x, y, 'gx')
plt.plot(x[self.best_coord], y[self.best_coord], 'o', color ='deepskyblue')
plt.plot(x, y_ransac, 'r-')
plt.legend(['Outliers','Inliers','RANSAC Estimated Curve'])
if show:
plt.show()
Solve and Visualize for 2nd Order#
# Load data
eqn = pd.read_csv("https://raw.githubusercontent.com/DL4CV-NPTEL/Deep-Learning-For-Computer-Vision/main/Data/Week%203/2nd_order.csv").to_numpy()
eqn = eqn[eqn[:, 0].argsort()]
x_2nd = eqn[:,0]
y_2nd = eqn[:,1]
np.set_printoptions(precision = 6)
# Find RANSAC model
ransac_2nd = Regression(2)
beta_2nd,error_2nd = ransac_2nd.solve(x_2nd, y_2nd, 2)
y_ransac_2nd = ransac_2nd.predict(x_2nd)
# Plot figures
ransac_2nd.visualize(x_2nd,y_2nd,y_ransac_2nd)
print("The coefficients are: ", beta_2nd)
print("The least square error is: {0:.6f}".format(error_2nd))
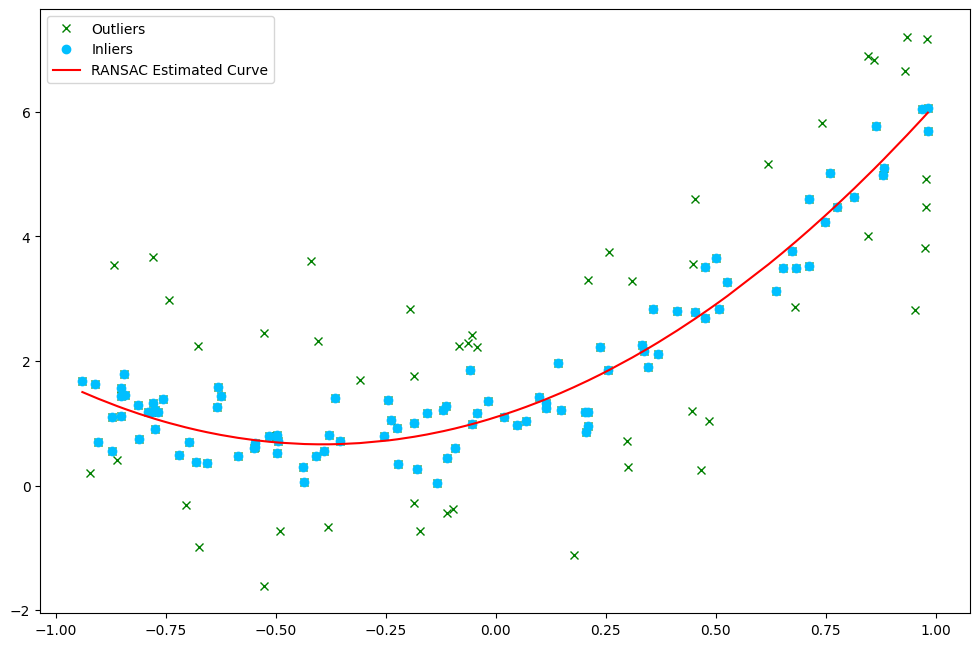
The coefficients are: [2.816757 2.215295 1.097521]
The least square error is: 0.150906