Lecture 6: CNNs for Human Understanding: Faces -Part 02 ^Code

#@title 
from ipywidgets import widgets
out1 = widgets.Output()
with out1:
  from IPython.display import YouTubeVideo
  video = YouTubeVideo(id=f"k4mNPA7WOVs", width=854, height=480, fs=1, rel=0)
  print("Video available at https://youtube.com/watch?v=" + video.id)
  display(video)
display(out1)

#@title 
from IPython import display as IPyDisplay
IPyDisplay.HTML(
    f"""
  <div>
    <a href= "https://github.com/DL4CV-NPTEL/Deep-Learning-For-Computer-Vision/blob/main/Slides/Week_7/DL4CV_Week07_Part04.pdf" target="_blank">
    <img src="https://github.com/DL4CV-NPTEL/Deep-Learning-For-Computer-Vision/blob/main/Data/Slides_Logo.png?raw=1"
  alt="button link to Airtable" style="width:200px"></a>
    </div>""" )

Imports

import torch
import torchvision
import torchvision.transforms as transforms

Feature learnings using contrastive learning on MNIST Dataset

from torchvision.datasets import MNIST
from torchvision import transforms

mean, std = 0.1307, 0.3081

train_dataset = MNIST('../data/MNIST', train=True, download=True,
                             transform=transforms.Compose([
                                 transforms.ToTensor(),
                                 transforms.Normalize((mean,), (std,))
                             ]))
test_dataset = MNIST('../data/MNIST', train=False, download=True,
                            transform=transforms.Compose([
                                transforms.ToTensor(),
                                transforms.Normalize((mean,), (std,))
                            ]))
n_classes = 10

Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-images-idx3-ubyte.gz to ../data/MNIST/MNIST/raw/train-images-idx3-ubyte.gz

Extracting ../data/MNIST/MNIST/raw/train-images-idx3-ubyte.gz to ../data/MNIST/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/train-labels-idx1-ubyte.gz to ../data/MNIST/MNIST/raw/train-labels-idx1-ubyte.gz

Extracting ../data/MNIST/MNIST/raw/train-labels-idx1-ubyte.gz to ../data/MNIST/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz
Downloading http://yann.lecun.com/exdb/mnist/t10k-images-idx3-ubyte.gz to ../data/MNIST/MNIST/raw/t10k-images-idx3-ubyte.gz

Extracting ../data/MNIST/MNIST/raw/t10k-images-idx3-ubyte.gz to ../data/MNIST/MNIST/raw

Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz

Downloading http://yann.lecun.com/exdb/mnist/t10k-labels-idx1-ubyte.gz to ../data/MNIST/MNIST/raw/t10k-labels-idx1-ubyte.gz

Extracting ../data/MNIST/MNIST/raw/t10k-labels-idx1-ubyte.gz to ../data/MNIST/MNIST/raw

Training Procedures

import torch
import numpy as np


def fit(train_loader, val_loader, model, loss_fn, optimizer, scheduler, n_epochs, cuda, log_interval, metrics=[],
        start_epoch=0):
    """
    Loaders, model, loss function and metrics should work together for a given task,
    i.e. The model should be able to process data output of loaders,
    loss function should process target output of loaders and outputs from the model

    Examples: Classification: batch loader, classification model, NLL loss, accuracy metric
    Siamese network: Siamese loader, siamese model, contrastive loss
    Online triplet learning: batch loader, embedding model, online triplet loss
    """
    for epoch in range(0, start_epoch):
        scheduler.step()

    for epoch in range(start_epoch, n_epochs):
        scheduler.step()

        # Train stage
        train_loss, metrics = train_epoch(train_loader, model, loss_fn, optimizer, cuda, log_interval, metrics)

        message = 'Epoch: {}/{}. Train set: Average loss: {:.4f}'.format(epoch + 1, n_epochs, train_loss)
        for metric in metrics:
            message += '\t{}: {}'.format(metric.name(), metric.value())

        val_loss, metrics = test_epoch(val_loader, model, loss_fn, cuda, metrics)
        val_loss /= len(val_loader)

        message += '\nEpoch: {}/{}. Validation set: Average loss: {:.4f}'.format(epoch + 1, n_epochs,
                                                                                 val_loss)
        for metric in metrics:
            message += '\t{}: {}'.format(metric.name(), metric.value())

        print(message)


def train_epoch(train_loader, model, loss_fn, optimizer, cuda, log_interval, metrics):
    for metric in metrics:
        metric.reset()

    model.train()
    losses = []
    total_loss = 0

    for batch_idx, (data, target) in enumerate(train_loader):
        target = target if len(target) > 0 else None
        if not type(data) in (tuple, list):
            data = (data,)
        if cuda:
            data = tuple(d.cuda() for d in data)
            if target is not None:
                target = target.cuda()


        optimizer.zero_grad()
        outputs = model(*data)

        if type(outputs) not in (tuple, list):
            outputs = (outputs,)

        loss_inputs = outputs
        if target is not None:
            target = (target,)
            loss_inputs += target

        loss_outputs = loss_fn(*loss_inputs)
        loss = loss_outputs[0] if type(loss_outputs) in (tuple, list) else loss_outputs
        losses.append(loss.item())
        total_loss += loss.item()
        loss.backward()
        optimizer.step()

        for metric in metrics:
            metric(outputs, target, loss_outputs)

        if batch_idx % log_interval == 0:
            message = 'Train: [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                batch_idx * len(data[0]), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), np.mean(losses))
            for metric in metrics:
                message += '\t{}: {}'.format(metric.name(), metric.value())

            print(message)
            losses = []

    total_loss /= (batch_idx + 1)
    return total_loss, metrics


def test_epoch(val_loader, model, loss_fn, cuda, metrics):
    with torch.no_grad():
        for metric in metrics:
            metric.reset()
        model.eval()
        val_loss = 0
        for batch_idx, (data, target) in enumerate(val_loader):
            target = target if len(target) > 0 else None
            if not type(data) in (tuple, list):
                data = (data,)
            if cuda:
                data = tuple(d.cuda() for d in data)
                if target is not None:
                    target = target.cuda()

            outputs = model(*data)

            if type(outputs) not in (tuple, list):
                outputs = (outputs,)
            loss_inputs = outputs
            if target is not None:
                target = (target,)
                loss_inputs += target

            loss_outputs = loss_fn(*loss_inputs)
            loss = loss_outputs[0] if type(loss_outputs) in (tuple, list) else loss_outputs
            val_loss += loss.item()

            for metric in metrics:
                metric(outputs, target, loss_outputs)

    return val_loss, metrics

Common Setup

import torch
from torch.optim import lr_scheduler
import torch.optim as optim
from torch.autograd import Variable
import numpy as np
cuda = torch.cuda.is_available()

%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt

mnist_classes = ['0', '1', '2', '3', '4', '5', '6', '7', '8', '9']
colors = ['#1f77b4', '#ff7f0e', '#2ca02c', '#d62728',
              '#9467bd', '#8c564b', '#e377c2', '#7f7f7f',
              '#bcbd22', '#17becf']

def plot_embeddings(embeddings, targets, xlim=None, ylim=None):
    plt.figure(figsize=(10,10))
    for i in range(10):
        inds = np.where(targets==i)[0]
        plt.scatter(embeddings[inds,0], embeddings[inds,1], alpha=0.5, color=colors[i])
    if xlim:
        plt.xlim(xlim[0], xlim[1])
    if ylim:
        plt.ylim(ylim[0], ylim[1])
    plt.legend(mnist_classes)

def extract_embeddings(dataloader, model):
    with torch.no_grad():
        model.eval()
        embeddings = np.zeros((len(dataloader.dataset), 2))
        labels = np.zeros(len(dataloader.dataset))
        k = 0
        for images, target in dataloader:
            if cuda:
                images = images.cuda()
            embeddings[k:k+len(images)] = model.get_embedding(images).data.cpu().numpy()
            labels[k:k+len(images)] = target.numpy()
            k += len(images)
    return embeddings, labels

Siamese network

from PIL import Image

from torch.utils.data import Dataset
from torch.utils.data.sampler import BatchSampler


class SiameseMNIST(Dataset):
    """
    Train: For each sample creates randomly a positive or a negative pair
    Test: Creates fixed pairs for testing
    """

    def __init__(self, mnist_dataset):
        self.mnist_dataset = mnist_dataset

        self.train = self.mnist_dataset.train
        self.transform = self.mnist_dataset.transform

        if self.train:
            self.train_labels = self.mnist_dataset.train_labels
            self.train_data = self.mnist_dataset.train_data
            self.labels_set = set(self.train_labels.numpy())
            self.label_to_indices = {label: np.where(self.train_labels.numpy() == label)[0]
                                     for label in self.labels_set}
        else:
            # generate fixed pairs for testing
            self.test_labels = self.mnist_dataset.test_labels
            self.test_data = self.mnist_dataset.test_data
            self.labels_set = set(self.test_labels.numpy())
            self.label_to_indices = {label: np.where(self.test_labels.numpy() == label)[0]
                                     for label in self.labels_set}

            random_state = np.random.RandomState(29)

            positive_pairs = [[i,
                               random_state.choice(self.label_to_indices[self.test_labels[i].item()]),
                               1]
                              for i in range(0, len(self.test_data), 2)]

            negative_pairs = [[i,
                               random_state.choice(self.label_to_indices[
                                                       np.random.choice(
                                                           list(self.labels_set - set([self.test_labels[i].item()]))
                                                       )
                                                   ]),
                               0]
                              for i in range(1, len(self.test_data), 2)]
            self.test_pairs = positive_pairs + negative_pairs

    def __getitem__(self, index):
        if self.train:
            target = np.random.randint(0, 2)
            img1, label1 = self.train_data[index], self.train_labels[index].item()
            if target == 1:
                siamese_index = index
                while siamese_index == index:
                    siamese_index = np.random.choice(self.label_to_indices[label1])
            else:
                siamese_label = np.random.choice(list(self.labels_set - set([label1])))
                siamese_index = np.random.choice(self.label_to_indices[siamese_label])
            img2 = self.train_data[siamese_index]
        else:
            img1 = self.test_data[self.test_pairs[index][0]]
            img2 = self.test_data[self.test_pairs[index][1]]
            target = self.test_pairs[index][2]

        img1 = Image.fromarray(img1.numpy(), mode='L')
        img2 = Image.fromarray(img2.numpy(), mode='L')
        if self.transform is not None:
            img1 = self.transform(img1)
            img2 = self.transform(img2)
        return (img1, img2), target

    def __len__(self):
        return len(self.mnist_dataset)

import torch.nn as nn
import torch.nn.functional as F


class EmbeddingNet(nn.Module):
    def __init__(self):
        super(EmbeddingNet, self).__init__()
        self.convnet = nn.Sequential(nn.Conv2d(1, 32, 5), nn.PReLU(),
                                     nn.MaxPool2d(2, stride=2),
                                     nn.Conv2d(32, 64, 5), nn.PReLU(),
                                     nn.MaxPool2d(2, stride=2))

        self.fc = nn.Sequential(nn.Linear(64 * 4 * 4, 256),
                                nn.PReLU(),
                                nn.Linear(256, 256),
                                nn.PReLU(),
                                nn.Linear(256, 2)
                                )

    def forward(self, x):
        output = self.convnet(x)
        output = output.view(output.size()[0], -1)
        output = self.fc(output)
        return output

    def get_embedding(self, x):
        return self.forward(x)


class EmbeddingNetL2(EmbeddingNet):
    def __init__(self):
        super(EmbeddingNetL2, self).__init__()

    def forward(self, x):
        output = super(EmbeddingNetL2, self).forward(x)
        output /= output.pow(2).sum(1, keepdim=True).sqrt()
        return output

    def get_embedding(self, x):
        return self.forward(x)


class ClassificationNet(nn.Module):
    def __init__(self, embedding_net, n_classes):
        super(ClassificationNet, self).__init__()
        self.embedding_net = embedding_net
        self.n_classes = n_classes
        self.nonlinear = nn.PReLU()
        self.fc1 = nn.Linear(2, n_classes)

    def forward(self, x):
        output = self.embedding_net(x)
        output = self.nonlinear(output)
        scores = F.log_softmax(self.fc1(output), dim=-1)
        return scores

    def get_embedding(self, x):
        return self.nonlinear(self.embedding_net(x))


class SiameseNet(nn.Module):
    def __init__(self, embedding_net):
        super(SiameseNet, self).__init__()
        self.embedding_net = embedding_net

    def forward(self, x1, x2):
        output1 = self.embedding_net(x1)
        output2 = self.embedding_net(x2)
        return output1, output2

    def get_embedding(self, x):
        return self.embedding_net(x)


class TripletNet(nn.Module):
    def __init__(self, embedding_net):
        super(TripletNet, self).__init__()
        self.embedding_net = embedding_net

    def forward(self, x1, x2, x3):
        output1 = self.embedding_net(x1)
        output2 = self.embedding_net(x2)
        output3 = self.embedding_net(x3)
        return output1, output2, output3

    def get_embedding(self, x):
        return self.embedding_net(x)

Siamese Network

Now we’ll train a siamese network that takes a pair of images and trains the embeddings so that the distance between them is minimized if their from the same class or greater than some margin value if they represent different classes. We’ll minimize a contrastive loss function(Raia Hadsell, Sumit Chopra, Yann LeCun, Dimensionality reduction by learning an invariant mapping, CVPR 2006): 

class ContrastiveLoss(nn.Module):
    """
    Contrastive loss
    Takes embeddings of two samples and a target label == 1 if samples are from the same class and label == 0 otherwise
    """

    def __init__(self, margin):
        super(ContrastiveLoss, self).__init__()
        self.margin = margin
        self.eps = 1e-9

    def forward(self, output1, output2, target, size_average=True):
        distances = (output2 - output1).pow(2).sum(1)  # squared distances
        losses = 0.5 * (target.float() * distances +
                        (1 + -1 * target).float() * F.relu(self.margin - (distances + self.eps).sqrt()).pow(2))
        return losses.mean() if size_average else losses.sum()

# Set up data loaders
siamese_train_dataset = SiameseMNIST(train_dataset) # Returns pairs of images and target same/different
siamese_test_dataset = SiameseMNIST(test_dataset)
batch_size = 128
kwargs = {'num_workers': 1, 'pin_memory': True} if cuda else {}
siamese_train_loader = torch.utils.data.DataLoader(siamese_train_dataset, batch_size=batch_size, shuffle=True, **kwargs)
siamese_test_loader = torch.utils.data.DataLoader(siamese_test_dataset, batch_size=batch_size, shuffle=False, **kwargs)

# Set up the network and training parameters
margin = 1.
embedding_net = EmbeddingNet()
model = SiameseNet(embedding_net)
if cuda:
    model.cuda()
loss_fn = ContrastiveLoss(margin)
lr = 1e-3
optimizer = optim.Adam(model.parameters(), lr=lr)
scheduler = lr_scheduler.StepLR(optimizer, 8, gamma=0.1, last_epoch=-1)
n_epochs = 5
log_interval = 100

/usr/local/lib/python3.7/dist-packages/torchvision/datasets/mnist.py:65: UserWarning: train_labels has been renamed targets
  warnings.warn("train_labels has been renamed targets")
/usr/local/lib/python3.7/dist-packages/torchvision/datasets/mnist.py:75: UserWarning: train_data has been renamed data
  warnings.warn("train_data has been renamed data")
/usr/local/lib/python3.7/dist-packages/torchvision/datasets/mnist.py:70: UserWarning: test_labels has been renamed targets
  warnings.warn("test_labels has been renamed targets")
/usr/local/lib/python3.7/dist-packages/torchvision/datasets/mnist.py:80: UserWarning: test_data has been renamed data
  warnings.warn("test_data has been renamed data")

fit(siamese_train_loader, siamese_test_loader, model, loss_fn, optimizer, scheduler, n_epochs, cuda, log_interval)

/usr/local/lib/python3.7/dist-packages/torch/optim/lr_scheduler.py:136: UserWarning: Detected call of `lr_scheduler.step()` before `optimizer.step()`. In PyTorch 1.1.0 and later, you should call them in the opposite order: `optimizer.step()` before `lr_scheduler.step()`.  Failure to do this will result in PyTorch skipping the first value of the learning rate schedule. See more details at https://pytorch.org/docs/stable/optim.html#how-to-adjust-learning-rate
  "https://pytorch.org/docs/stable/optim.html#how-to-adjust-learning-rate", UserWarning)

Train: [0/60000 (0%)]	Loss: 0.214045

Train: [12800/60000 (21%)]	Loss: 0.070558

Train: [25600/60000 (43%)]	Loss: 0.039938

Train: [38400/60000 (64%)]	Loss: 0.029317

Train: [51200/60000 (85%)]	Loss: 0.021358

Epoch: 1/5. Train set: Average loss: 0.0376
Epoch: 1/5. Validation set: Average loss: 0.0179

Train: [0/60000 (0%)]	Loss: 0.018129

Train: [12800/60000 (21%)]	Loss: 0.017003

Train: [25600/60000 (43%)]	Loss: 0.014276

Train: [38400/60000 (64%)]	Loss: 0.012290

Train: [51200/60000 (85%)]	Loss: 0.011505

Epoch: 2/5. Train set: Average loss: 0.0130
Epoch: 2/5. Validation set: Average loss: 0.0095

Train: [0/60000 (0%)]	Loss: 0.007402

Train: [12800/60000 (21%)]	Loss: 0.009552

Train: [25600/60000 (43%)]	Loss: 0.008338

Train: [38400/60000 (64%)]	Loss: 0.007823

Train: [51200/60000 (85%)]	Loss: 0.006631

Epoch: 3/5. Train set: Average loss: 0.0081
Epoch: 3/5. Validation set: Average loss: 0.0073

Train: [0/60000 (0%)]	Loss: 0.007715

Train: [12800/60000 (21%)]	Loss: 0.007476

Train: [25600/60000 (43%)]	Loss: 0.004673

Train: [38400/60000 (64%)]	Loss: 0.005973

Train: [51200/60000 (85%)]	Loss: 0.004725

Epoch: 4/5. Train set: Average loss: 0.0057
Epoch: 4/5. Validation set: Average loss: 0.0063

Train: [0/60000 (0%)]	Loss: 0.005345

Train: [12800/60000 (21%)]	Loss: 0.004021

Train: [25600/60000 (43%)]	Loss: 0.004697

Train: [38400/60000 (64%)]	Loss: 0.003915

Train: [51200/60000 (85%)]	Loss: 0.003818

Epoch: 5/5. Train set: Average loss: 0.0042
Epoch: 5/5. Validation set: Average loss: 0.0056

# Set up data loaders
batch_size = 256
kwargs = {'num_workers': 1, 'pin_memory': True} if cuda else {}
train_loader = torch.utils.data.DataLoader(train_dataset, batch_size=batch_size, shuffle=True, **kwargs)
test_loader = torch.utils.data.DataLoader(test_dataset, batch_size=batch_size, shuffle=False, **kwargs)


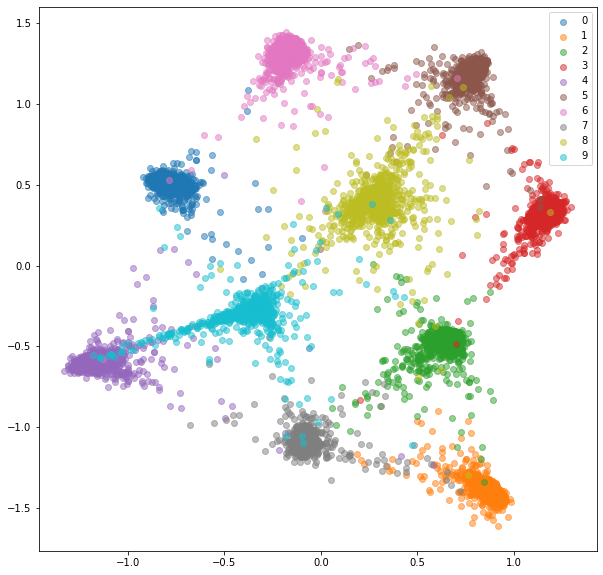
train_embeddings_cl, train_labels_cl = extract_embeddings(train_loader, model)
plot_embeddings(train_embeddings_cl, train_labels_cl)
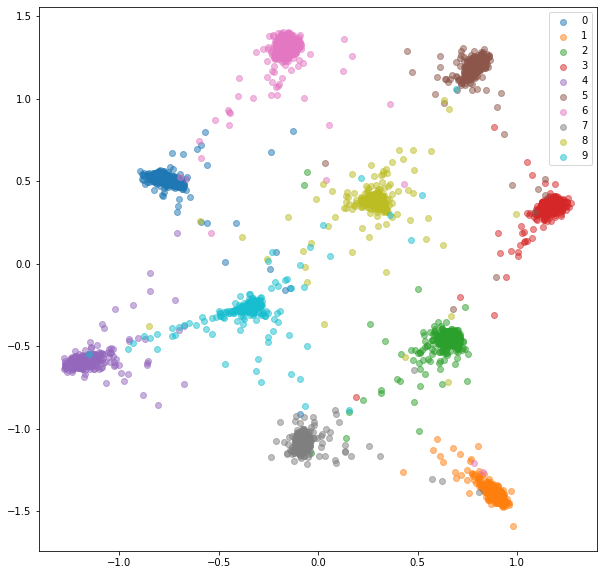
val_embeddings_cl, val_labels_cl = extract_embeddings(test_loader, model)
plot_embeddings(val_embeddings_cl, val_labels_cl)